Parallel Solution of the 3-D Navier-Stokes Equations on Unstructured Meshes
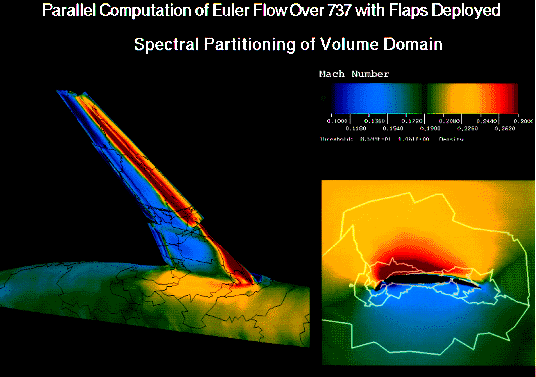

Objective: Develop a parallel numerical solution procedure for solving the three-dimensional compressible Navier-Stokes equations on arbitrary unstructured meshes.
Approach: The compressible Navier-Stokes equations governing high speed fluid flow are approximated by a finite volume numerical discretization technique on tetrahedral elements. The use of tetrahedral elements has proven advantageous in simplifying computations for complex spatial domains. The discretization technique yields are a large system of coupled nonlinear equations which are solved using a Newton-like iteration. Each Newton iteration requires the solution of a large sparse linear system of algebraic equations.
We have developed a parallel solution strategy in which the problem domain is decomposed and distributed among processors of the parallel computer. The large system of linear algebraic equations is solved using a generalized minimum residual algorithm which utilizes a message passing protocol to achieve results identical to that obtained if the problem were solved on a single processor. To enhance the convergence characteristics of the minimum residual solver, a domain decomposed variant of incomplete lower-upper (ILU) factorization is used to precondition the linear system. The domain decomposed ILU factorization requires that each processor solve a smaller sparse linear system of equations followed by interprocessor information exchange using a message passing protocol.
Accomplishment: A prototype FORTRAN code utilizing MPI message passing protocol is under development for the IBM SP2. Preliminary testing of the code for inviscid Euler equations has been successful and final incorporation of code modules for the Navier-Stokes equations is nearing completion. Results of this work will be reported at the AIAA Aerospace sciences meeting January 9, 1995 (AIAA paper 95-0221).
Significance: The development of a Newton solver strategy should provide a useful tool for fluid flow analysis as well as a sound basis for the development and research into a number of new emerging areas of research: shape optimization and design, homotopy analysis of fluid bifurcation problems, and studies of fluid flow stability and transition.
Point of Contact:
 Return to the Table of Contents
Return to the Table of Contents