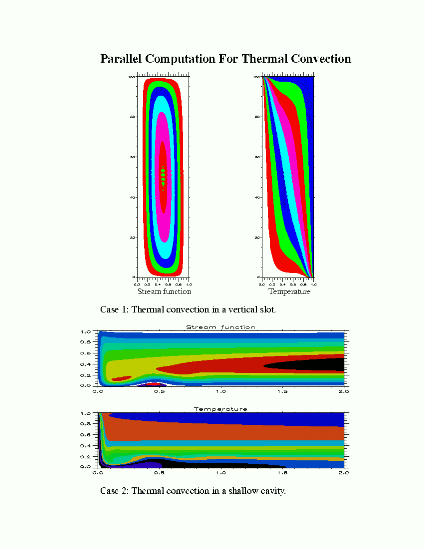
Approach: In order to determine such flow structures and heat transfer, numerical simulations for the Navier-Stokes equations and the Heat equations will be considered on the Intel Touchstone Delta, the Intel Paragon, and the Cray T3D. The finite difference method is used for the whole computation for two-dimensional problems. The Dufor-Frankel Method is applied for the Energy equation and the Vorticity equation, which is an explicit, three-layer method and has second-order accuracy. The Multigrid method is used for the Poisson equation, which is based on a five-point scheme and Successive Over-Relaxation method. This has proven to be an effective and fast method. In present code, a complete V-Cycle scheme is used for the time-dependent problem.
Accomplishments: A parallel computation code for natural convective flows has been implemented on different parallel systems. Finite-difference method, multigrid method, DuFort-Frankel method, and domain decomposition techniques have been used in this code. The code has been tested for different Rayleigh numbers and Prandtl numbers, and new numerical solutions are obtained for a large range of Rayleigh numbers, Prandtl numbers, and aspect ratios. Numerical results are in excellent agreement with theoretical predictions. The parallel code is numerically stable, computationally efficient, and portable to various parallel architectures which support either PVM or NX libraries for communications.
Significance: Convective motions driven by lateral temperature gradients are important in many areas of interest in industry and in nature. Applications include the temperature control of circuit board components under natural convection in the electronics industry, heating and ventilation control in building design and construction, cooling systems for nuclear reactors in the nuclear industry, solar-energy collectors in the power industry and atmospheric and fluvial dispersion in the environment.
Status/Plans: The present implementation of two-dimensional thermal convection problems has been used with various physical properties. An efficient and practical numerical approach for three dimensional flow problems is under investigation. This implementation is based on a widely used finite volume method for predicting incompressible fluid flows, which provided a remarkably successful implicit method. The discretized equations are solved by the most efficient and fastest iterative method, the Multigrid scheme with the Successive Over-Relaxation as the smoother. The sequential code is finished, and it gives prospective results. More numerical tests for large grid sizes, the optimization of the code, and the parallelization to various parallel systems are underway.
Point of Contact:
Ping Wang
Jet Propulsion Laboratory
wangp@rockymt.jpl.nasa.gov
(818) 393-1941