NASA
High Performance Computing
and Communications Program
Computational AeroSciences Project
Optimal Scheduling for Reduction of Complex Systems
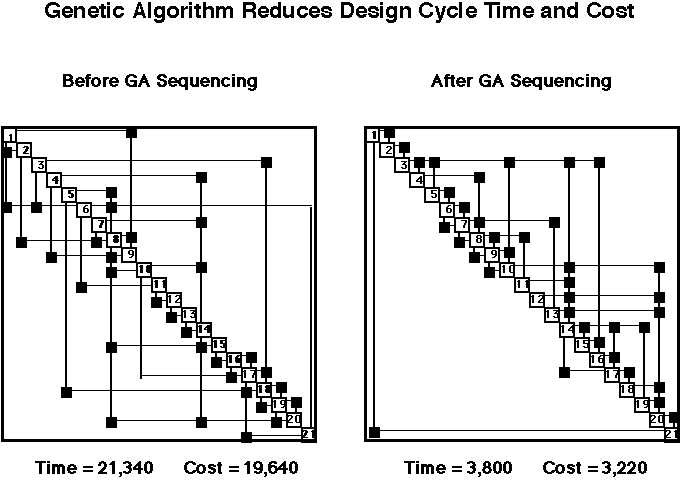
Objective: The objective of this research is to develop optimal sequencing strategies for reducing both the time and cost of the analysis and design process for complex engineering systems, such as those that are encountered in Multidisciplinary Design Optimization (MDO). One obstacle to the full implementation of MDO in an industrial setting is the considerable computational requirement that arises from the large number of participating coupled processes. The number of couplings (off-diagonal boxes in the figure) among these processes (diagonal elements in the figure) is so great that formal optimization methods cannot be applied directly. The present work focuses on using sensitivity-based coupling-strength strategies together with a discrete optimization approach via genetic algorithms (GA's) to perform an optimal sequencing of design processes, with the goal of increasing efficiency and reducing computational times and design-cycle costs.
Approach: An objective function incorporating user-prescribed criteria was formulated which includes terms to minimize cost and/or time. The design variables were expressed in such a manner to specify uniquely the position of each process of the design structure matrix. Because a finite number of possible orderings exists for a finite number of processes, the scheduling problem is discrete. The discrete nature of the sequencing problem facilitates solution by GA's. These GA's are both efficient and robust in a discrete search for an optimum; this conclusion is supported by many prior investigations. The following studies were performed as part of this research effort: an investigation of different codings for the GA-based sequencing (the first using a binary set of variables and the second using a direct-sequence to represent the modules), a stochastic study to determine feasible GA parameter settings (e.g., mutation rate, crossover selection mechanism, initial population size), a stochastic investigation of the impact of coupling densities on GA-based sequencing performance, and parametric studies to investigate the impact of weighting-term variations in the objective function.
Accomplishments: This work demonstrates that the incorporation of a GA sequencer into iterative subcycles of the design cycle increases efficiency and reduces the solution time. Results have demonstrated that a design-space that captures the direct sequence of the processes should be used, rather than a binary coding. Further, a multiobjective functional with weightings (between 0 and 1) for cost and time, should be used for the GA objective function. The required initial population size, as well as other GA parameters, can be determined by using a heuristic which is developed from the stochastic studies based on the coupling densities and the number of design processes.
Significance: Optimal sequencing can substantially decrease both the cost and/or time for complex engineering analysis and design as shown in the figure. Once this sequence is known, it can be applied to control the order in which processes are executed in an MDO framework.
Status/Plans: The GA-based sequencer will be extended to incorporate convergence strategies that minimize the cost and/or time of analysis and design processes. It will also be extended to identify weak couplings that could be artifically removed (either completely or else during just part of the convergence process) without adversely impacting the final result to increase the opportunities for parallel execution.
C. L. Bloebaum & C. M. McCulley
SUNY, Buffalo
(716) 645-2199
email: clb@eng.buffalo.edu
J. L. Rogers
NASA Langley Research Center
(804) 864-2810
email : j.l.rogers@larc.nasa.gov