
Approach: In order to determine such flow structures and heat transfer, numerical simulation for the Navier-Stokes equations and the Heat equations will be considered on the Intel Paragon, the Cray T3D, and the IBM SP2. The finite volume method is used for the whole computation for three-dimensional problems. The discretization equations derived from the scheme, including a pressure equation which consumes most of computation time, are solved using a parallel Multigrid method. A flexible parallel code has been implemented on the Intel Paragon, the Cray T3D, and the IBM SP2 by using domain decomposition techniques and the MPI or NX communication software.
Accomplishments: A parallel computation code for thermal convective flows has been implemented on different parallel systems. Finite-volume method, multigrid method, and domain decomposition techniques have been used in this code. The code has been tested for different Rayleigh numbers and Prandtl numbers, and new numerical solutions are obtained for a large range of Rayleigh numbers. The code can use 1D, 2D, or 3D partitions according to different geometries. It is numerically stable, computationally efficient, and portable to various parallel architectures which support either MPI or NX libraries for communications.
Significance: Convective motions driven by lateral temperature gradients are important in many areas of interest in industry and in nature. Applications include the temperature control of circuit board components under natural convection in the electronics industry, heating and ventilation control in building design and construction, cooling systems for nuclear reactors in the nuclear industry, solar-energy collectors in the power industry, and atmospheric and fluvial dispersion in the environment.
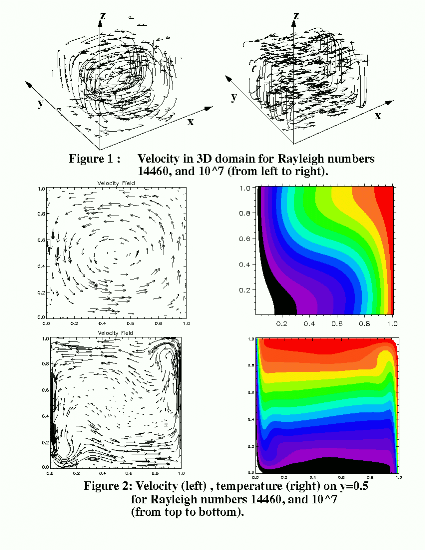
Status/Plans: The present code for three-dimensional thermal convection problems has been tested with various physical properties. Our present results clearly demonstrate the great potential for applying this approach to solving high Rayleigh number flows in realistic, three-dimensional geometries using parallel systems with large gird sizes. Much higher Rayleigh numbers computations and transient features of thermal convection in 3D are under investigation.
Point of Contact:
Ping Wang
Jet Propulsion Laboratory
wangp@rockymt.jpl.nasa.gov
(818) 393-1941