LICZBY RZECZYWISTE

W zbiorze liczb wymiernych okre£lamy dzia│ania A , ─ , ù w spos≤b nastΩpuj╣cy:

aA b=a+b+1

a─ b=a+b+ab

ao b=(a+b)/2

Elementem neutralnym (modu│em) dodawania jest liczba zero. x+0=x

Elementem neutralnym (modu│em)mno┐enia jest liczba 1. x*1=x

Dzia│ania na pierwiastkach:

; a3 0 i b3 0

gdzie a3 0 i b3 0

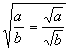
gdzie a3 0 i b>0

Pierwiastek nieparzystego stopnia z liczby a<0 okre£lamy:

Dzia│ania na potΩgach:

dla a1 0 i m3 n

dla b1 0

dla n╬ N i a3 0

dla n╬ N i a3 0

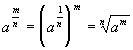
dla a3 0 i m, n╬ N

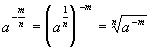
dla a>0 i m, n╬ N

Wzory skr≤conego mno┐enia:

kwadrat sumy

(a+b)²=a²+2ab+b²

kwadrat r≤┐nicy

(a-b)²=a²-2ab+b²

sze£cian sumy

(a+b)³=a³+3a²b+3ab²+b³

sze£cian r≤┐nicy

(a-b)³=a³-3a²b+3ab²-b³

r≤┐nica kwadrat≤w

a²-b²=(a+b(a-b)

r≤┐nica sze£cian≤w

a³-b³=(a-b)(a²+ab+b²)

suma sze£cian≤w

a³+b³=(a+b)(a²-ab+b²)

Warto£µ bezwzglΩdna:

Warto£ci╣ bezwzglΩdn╣ z liczby nieujemnej jest liczba nieujemna, a z liczby ujemnej liczba dodatnia.

Je£li x nale┐y do R ? |x|3 0.

|x|=xU x3 0

|x|=-xU x<0

W│asno£ci warto£ci bezwzglΩdnej:

1. x╬ R? |x|3 0

2. |x|<aU -a<x<aU x>-a; x<a

3. |x|L aU aL xL a

4. |x|>aU x>a lub x<-a

5. |x|3 aU x3 a lub xL -a

6. |x+y|L |x|+|y|

7. |x+y|3 |x|-|y|

8. |x*y|=|x|*|y|

9. |x/y|=|x|/|y|