
Expression controllers are another way to control animation. They let you use mathematical expressions to:
An expression is a mathematical function that returns a single value. 3D Studio MAX evaluates the expression once for each frame of an animation, generating values that can change from frame to frame.
You create and manage expression controllers in Track View. You can assign expressions to the following kinds of animation controllers:
Any numeric creation parameter
Position [X, Y, Z]
X Rotation
Y Rotation
Z Rotation
Scale [X%, Y%, Z%]
Any numeric modifier parameter (including creation parameters)
Colors [R, G, B]
Any numeric material parameter
Note: Expression controllers can work only with the individual XYZ components of Euler rotation. You can’t assign an expression to TCB rotation or other kinds of rotation controllers.
The type of value returned by an expression depends on the kind of controller:
If the parameter has an integer value, the expression rounds the float value to the nearest integer.
In the following tables, p and q are any scalar value or expression, V and W are any vector value or expression. (The character “x” is used as the vector cross-product operator.)
These are the arithmetic operators for scalar values:
+ p+q addition
- p-q subtraction
- -p additive inverse
* p*q multiplication
/ p/q division
^
p^q
power (p to the power of q);
**
p**q
^ and ** are the same operation
You can also use logical (Boolean) operators with scalar values. These operators all return 1 if true, 0 otherwise:
= p=q equal to
< p<q less than
> p>q greater than
<= p<=q less than or equal to
>= p>=q greater than or equal to
| p|q logical OR, returns 1 if either p or q is non-zero; otherwise, returns 0
& p&q logical AND, returns 1 if p and q are both non-zero; otherwise, returns 0
Note: Logical operators are useful with the “if” function.
For vectors that have a variable name, you can use a special component operator (.) to refer to the three scalar components of the vector:
V.x first component (X)
V.y second component (Y)
V.z third component (Z)
These are the operators for vector arithmetic:
+ V+W addition
- V-W subtraction
*
p*V
scalar multiplication
V*p
* V*W dot product
x VxW cross product
/ V/p scalar division
3D Studio MAX expressions use eight levels of precedence. The higher the operator is on the list the earlier it is evaluated.
- + as unary operators~e.g., -8, +25
. the component operator-as in V.x
** ^
x cross product
* /
+ -
= < > <= >=
| &
Parentheses are a special case. They are a grouping or subexpression operator that is provided so you can override the precedence order of the other operators.
In 3D Studio MAX expressions, variables are represented by symbolic names. You create them to contain constant or variable values in your expressions. 3D Studio MAX also provides several predefined variables that have constant or variable values.
These are the predefined variables that have a constant value in 3D Studio MAX expressions (variable names are case-sensitive):
pi 3.14159... Ratio of a circle’s circumference to its diameter.
e 2.71828... Base of natural logarithms.
TPS 4800 Ticks per second~the basic time unit of 3D Studio MAX animation.
These are the predefined variables that have a variable, time-based value in 3D Studio MAX expressions (variable names are case sensitive):
F Frame number.
For each frame, F equals the current frame number, counting from zero. The range of frames can vary depending on the number of frames in the active time segment.
NT Normalized time.
By definition, normalized time (NT) ranges from 0 to 1 over the active time segment, regardless of how many frames are in the segment. If you base an expression on NT, its effect happens exactly once over the range . You can also multiply NT by a factor to cause the expression’s effect to happen a certain number of times (for example, 2*NT causes the expression’s effect to happen twice).
Expressions based on NT speed up or slow down if you later change the length of the time segment.
S Seconds (elapsed time in seconds).
Elapsed time is measured from the first frame to the current frame. The range of seconds can vary depending on the total time of the active time segment.
T Ticks (elapsed time in ticks).
There are 4800 ticks per second. Elapsed time is measured from the first frame to the current frame. The range of ticks can vary depending on the total time of the active time segment.
You can create a variable whose value varies over time by assigning a controller to it. The controller must be one of the tracks of a different object. The value of the user-defined variable will then vary according to how the other object’s track varies over time.
There is one exception to the rule that the controller must belong to a different object; you can also assign Transform expressions to the same object’s base parameters, and vice versa.
You can assign vector variables to objects as well as controllers, making the result of the expression absolute to the local object. The value returned is the absolute value of the object relative to the world.
When you click the Assign to Controller button, the hierarchy list appears with the valid controller and the valid objects in bolded text.
Use Global Tracks in the Track View hierarchy to create global variables. Using expression controllers, you can point to a controller in the Global Tracks from several other tracks. Then, to change all of the other tracks, simply alter the expression in the Global Tracks.
Following is a list of functions provided for 3D Studio MAX expressions. In this list, p, q, and r represent scalar values or scalar expressions; V and W represent vector values or vector expressions.
To use a function in an expression, enter the name of the function and appropriate arguments to it.
The sine, cosine, and tangent functions take an angle in degrees and return a floating-point value. The arc functions take a floating-point value and return a value in degrees.
sin(p) sine
cos(p) cosine
tan(p) tangent
asin(p) arc sine
acos(p) arc cosine
atan(p) arc tangent
Hyperbolic functions take a floating-point value and return a floating-point value.
sinh(p) hyperbolic sine
cosh(p) hyperbolic cosine
tanh(p) hyperbolic tangent
radToDeg(p) takes p in radians and returns the same angle in degrees
degToRad(p) takes p in degrees and returns the same angle in radians
ceil(p) smallest integer greater than or equal to p
floor(p) largest integer less than or equal to p
ln(p) natural (base e) logarithm
log(p) common (base 10) logarithm
exp(p) exponential function exp(p) = e^p
pow(p,q) p to the power of q (p^q)
sqrt(p) square root
abs(p) absolute value
min(p,q) minimum returns p or q, depending on which is smaller
max(p,q) maximum returns p or q, depending on which is greater
mod(p,q) remainder of p divided by q
if(p,q,r)
works like the common spreadsheet “if”. If p is non-zero then “if”
returns q, otherwise “if” returns r.
vif(c,V1,V2) "Vector If". Value is V1 if c is true, else V2
length(V) the length of V
comp(V,i) i’th component (I=0,1,2)~comp([5,6,7],1)=6
unit(V) returns a unit vector in the same direction as V
Note: The comp function is an alternative to the notation V.x, V.y, V.z.
Noise(p,q,r) 3D noise, returns a randomly generated position
p,q and r are arbitrary values used as a random-generation seed; re-use these values to ensure that noise() returns the same value
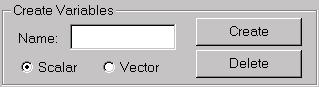
Name: Enter a name in this field. This is the first step in creating a variable.
Scalar: Select the type of variable to be created.
Vector: Select the type of variable to be created.
Create: Click to create a variable.
You must enter a name and specify a type before using the Create button.
Delete: Select a variable in the Scalars or Vectors list, then click Delete to delete the variable.

Tick Offset: Enter an offset value in the Tick Offset field.
A tick is 1/4800 of a second. If a variable has a non-zero tick offset, that value is added to the current time before the controller track is evaluated.
Assign a constant value to a variable.
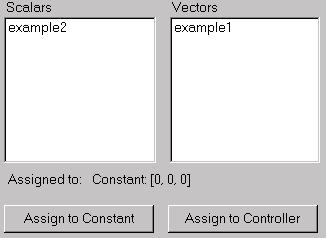
Assign a controller to a variable.
The Track View Pick subdialog appears, showing the track hierarchy. The display in the dialog is like the Hierarchy window of Track View itself.
Type an expression in the Expression box.
The expression must be a valid mathematical expression that evaluates to the proper type, its result is either a three-value vector for a vector expression (position, scale, or point3) or a scalar value for a float expression.
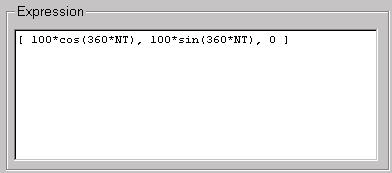
Enter text in this area to document an expression.
Describe user-defined variables, for example.
Function list: Displays a list of expression controller functions.
In the Function list, p, q, and r represent scalar values or scalar expressions; V and W represent vector values or vector expressions.
Save: Save an expression.
Expressions are saved as files with a .xpr filename extension.
Load: Load an expression.
A saved expression does not save variable definitions or values. After loading the expression, you need to redefine them.
Debug: Display the Expression Debug window.
This window displays the values of all variables, plus the value of the expression itself. When you change the variables or move the time slider, the debug window automatically updates so you can interactively view what’s happening with the expression. Also displayed are the values for frames (F), normalized time (NT), secs (S), and ticks (T).
Evaluate: Evaluate the expression for each frame in the animation.
There is no explicit assignment (= or := operator) as in a conventional programming language, the assignment is implicit, and takes place over time.
If there is a syntax error in the expression, an alert box displays an error message. The error message is the first part of the expression itself. The last character in the error message is the point at which the evaluator detected the error. This is usually where the error actually is, unless the problem is that opening and closing parentheses (or the braces for vectors) don’t match up. In this case, evaluation may proceed further through the expression before it detects the error.
Close: Close the expression controller dialog.
Use Track View to create the expression controller.
The Choose Controller dialog appears.
Use the Expression Controller dialog to create the expression.
The Expression Controller dialog appears.
[ 100*cos(360*NT), 100*sin(360*NT), 0 ]
Play the animation. The sphere moves in a circle about the world origin (0,0,0). The radius of the circular path is 100 units.
You’ve now specified a circular path for the sphere. NT is a variable that means normalized time. Movement based on NT happens exactly once per the active time segment, regardless of how many frames are in the animation.
The two 100s in the expression specify the radius. To adjust the radius of the circle’s path, create a symbolic variable to represent the radius. The variable has a constant value that is easy to edit.
The name radius appears in the Scalars list in the lower-left part of the dialog.
A dialog titled radius appears.
The radius variable now equals 150.
Now use the new variable in the expression.
[ radius*cos(360*NT), radius*sin(360*NT), 0]
Play the animation. The sphere moves in a circle about the world origin (0,0,0). The radius of the circular path is 150 units.
Now make the sphere rotate about a box:
The name boxposn appears in the Vectors list in the lower-left part of the dialog.
Variable names are case sensitive; the variable name should be lower case.
The Track View Pick dialog appears. It shows the object hierarchy as it appears in the left side of Track View.
[ radius * cos(360*NT),
radius * sin(360*NT), 0] + boxposn
Play the animation again. The sphere moves in a circle around the box while following the box wherever it moves.