Das Zeichnen von Polynomen und Polygonen

Zwei Arten von Kurven in der Ebene werden häufig zur Darstellung von Grafiken verwendet und sollen deshalb eigens erwähnt werden, nämlich Polynome und Polygone. Ein Polynom in der Ebene ist gegeben durch

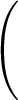
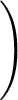
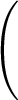
$\displaystyle \left(\vphantom{\begin{array}{cc} x\\ y\end{array}}\right.$$\displaystyle \begin{array}{cc} x\\ y\end{array}$$\displaystyle \left.\vphantom{\begin{array}{cc} x\\ y\end{array}}\right)$ = $\displaystyle \left(\vphantom{\begin{array}{ll} a_0 + a_1 t + a_2 t^2 + \ldots\\ b_0 + b_1 t + b_2 t^2 + \ldots \end{array}}\right.$$\displaystyle \begin{array}{ll} a_0 + a_1 t + a_2 t^2 + \ldots\\ b_0 + b_1 t + b_2 t^2 + \ldots \end{array}$$\displaystyle \left.\vphantom{\begin{array}{ll} a_0 + a_1 t + a_2 t^2 + \ldots\\ b_0 + b_1 t + b_2 t^2 + \ldots \end{array}}\right)$ ,

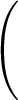
wobei n Punkte bei den äquidistanten Parameterwerten ts + (i⋅((te - ts)/(n - 1)))    0≤i≤n - 1 berechnet werden. Durch Verwendung eines Wiederholfaktors läßt sich ein solches Polynom sehr einfach darstellen. Der Parameterbereich wird durch den Bezeichner im Wiederholfaktor abgedeckt und die Polynomgleichung wird einfach zur Berechnung der Offsets herangezogen. Als Beispiel ist das Polynom

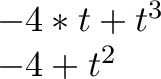$\displaystyle \left(\vphantom{\begin{array}{cc} x\\ y\end{array}}\right.$$\displaystyle \begin{array}{cc} x\\ y\end{array}$$\displaystyle \left.\vphantom{\begin{array}{cc} x\\ y\end{array}}\right)$ = $\displaystyle \left(\vphantom{\begin{array}{ll} -4*t+t^3\\ -4+t^2\\ \end{array}}\right.$$\displaystyle \begin{array}{ll} -4*t+t^3\\ -4+t^2\\ \end{array}$$\displaystyle \left.\vphantom{\begin{array}{ll} -4*t+t^3\\ -4+t^2\\ \end{array}}\right)$ ,

in Abbildung A.18 zu sehen. Der zugehörige LATEX-Code ist: 

\setdefaults\setunitlength{1cm}
\begin{picture}(12,7)
\special{gr setdotsize 2pt}
\put(6,4){
 \special{gr setpoint 0 t=-2.5..2.5:16[-4*t+t*t*t,-4+t*t];
             dot 0-15; spline 0-15; }}
\end{picture}

Abbildung: Ein setpoint Polynom
\begin{figure}\centering \setdefaults\setunitlength{1cm} \begin{picture}(12,7) \... ....2.5:16[-4*t+t*t*t,-4+t*t]; dot 0-15; spline 0-15; }} \end{picture}\end{figure}

Ein (evtl. offenes) Polygon wird dadurch erzeugt, daß man zu einem gegebenen Startpunkt x, y die Seitenlänge l und einen Startwinkel α sowie einen Winkel β, der bei jedem erzeugten Punkt auf den bisherigen Winkel aufaddiert wird, angibt. Links sehen Sie ein Beispiel, in dem die entsprechenden Parameter in einer Zeichnung verdeutlicht werden. 1pt
\begin{picture}(90,90) \put(0,0){\special{gr def p1=360/5*pi/180/2; def p0=10*p... ...}} \put(74,45){\makebox(0,0){$l$}} \put(45,11){\makebox(0,0){$l$}} \end{picture}

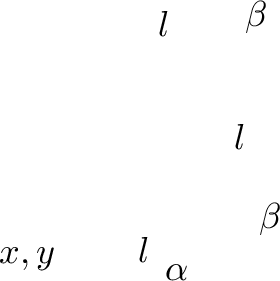
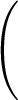
Als eine Art Kochrezept zum Zeichnen von Polygonen kann folgendes Vorgehen dienen. Für ein Polygon, das durch n Punkte definiert werden soll, erzeugt man sich n Punkte zi = 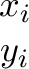$\left(\vphantom{\begin{array}{cc}x_i\\ y_i\\ \end{array}}\right.$$\begin{array}{cc}x_i\\ y_i\\ \end{array}$$\left.\vphantom{\begin{array}{cc}x_i\\ y_i\\ \end{array}}\right)$ durch die Iterationsvorschrift

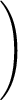
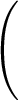
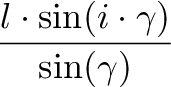
zi = $\displaystyle \left(\vphantom{\begin{array}{cc}x\\ y\\ \end{array}}\right.$$\displaystyle \begin{array}{cc}x\\ y\\ \end{array}$$\displaystyle \left.\vphantom{\begin{array}{cc}x\\ y\\ \end{array}}\right)$ + $\displaystyle {\frac{{l\cdot \sin(i\cdot \gamma)}}{{\sin(\gamma)}}}$⋅$\displaystyle \left(\vphantom{\begin{array}{rr}\cos((1-i)\cdot \gamma -\alpha)\\ -\sin((1-i)\cdot \gamma - \alpha)\\ \end{array}}\right.$$\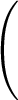displaystyle \begin{array}{rr}\cos((1-i)\cdot \gamma -\alpha)\\ -\sin((1-i)\cdot \gamma - \alpha)\\ \end{array}$$\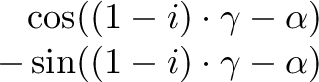displaystyle \left.\vphantom{\begin{array}{rr}\cos((1-i)\cdot \gamma -\alpha)\\ -\sin((1-i)\cdot \gamma - \alpha)\\ \end{array}}\right)$    ,

wobei der Parameter i im Bereich 0≤i≤n - 1 an den n äquidistanten Stellen 0, 1,...n - 1 eingesetzt wird und der Winkel γ sich berechnet zu γ = 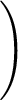${\frac{{\beta}}{{2}}}$.

Mit den Parametern α = 10o, β = 360/5o, l = 60, n = 5 und 1pt
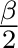
\begin{picture}(90,90) \put(0,0){\special{gr def p1=360/5*pi/180/2; def p0=10*p... ...ize 5 pt; dot 2; setdotsize 6 pt; dot 3; setdotsize 7 pt; dot 4}} \end{picture}
dem Startpunkt x = 15, y = 0 ergibt sich das regelmäßige Fünfeck links. Die Eckpunkte sind in der Reihenfolge ihrer Erzeugung jeweils etwas größer gezeichnet. Der zugehörige LATEX-Code ist folgender. Bitte beachten Sie, daß die Winkelangaben in Grad für die Treiber ins Bogenmaß umgerechnet werden müssen. Deshalb das merkwürdige Aussehen der Formeln. 

\setdefaults\setunitlength{1pt}
\begin{picture}(90,90)
\put(0,0){\special{gr def p1=360/5*pi/180/2;
  def p0=10*pi/180;
  def x0=15; def y0=0; def l=60;
  setpoint 0 t=0..4:5[
    x0+l*sin(t*p1)/sin(p1)*cos((1-t)*p1-p0),
    y0-l*sin(t*p1)/sin(p1)*sin((1-t)*p1-p0)];
  closedpoly 0-4;
  setdotsize 3 pt; dot 0; setdotsize 4 pt; dot 1;
  setdotsize 5 pt; dot 2; setdotsize 6 pt; dot 3;
  setdotsize 7 pt; dot 4}}
\end{picture}